瘋録

以前からワイドショーの類はあまり見なかったのですが
地デジのテレビは昨年暮れにようやく購入したのもあり
すっかりテレビを見なくなりました。
そのせいか、STAP細胞が注目され始めた当初
割烹着姿で話題になった頃を知りません。
一応はSTAP細胞の概略は読みましたが、
その頃から「いずれ詳しい解説書が出るから
その時に読めばいい」くらいに思っていました。

病院でMRIの経験のある方も少なくないと思いますが
MRI関連で最初のノーベル賞は2003年のことです。
ノーベル賞は実績が出てから評価されるまでの期間が長く
「生きていることも最大の受賞要件」なんて言われるほどです。

さて、皆さんは存在するかどうか分からないSTAP細胞より
実績が確実にあるMRIを詳しく説明できますか?

新聞やテレビでも連日のように騒がれていますが
もっと他に注目すべきことはあるのではないでしょうか?  

中秋の名月の頃に書いたことに、
ちょっと確信を得られなかったことがあったので
求めてみることにしました。

それは、新月から満月までの時間が
朔望月29.53日の半分より
どれだけ短くなったり長くなったりするのかです。
朔望月については以前のブログをご覧ください。

朔望月について考えるのは大変なので
今回は月が半周するのにかかる時間が
公転周期の半分に対してどれだけ
短くなったり長くなったりするのかを求めて
代用することにします。
(ここでの半周とは「一周の半分」という意味ではなく
「公転の中心となる星から見て正反対の位置に
来る」という意味であるとします)

先日の時計の例えで言うならば
時計の長針と短針が重なってから反対向きに
なるまでの時間を計算するのは大変なので
単純に時計の長針が半周する時間を求める
だけに留めるということです。

ここで、楕円について少し触れておきます。
楕円は「2点F₁,F₂からの距離の和が等しい点の集合」ですが
この2点F₁,F₂を「焦点」と呼び
公転の中心となる星は焦点のどちらか一方になります。
楕円には長軸ABと短軸CDがあり、
長軸の長さの半分を「長径」とか「平均半径」と呼びます。
楕円の中心から焦点までの距離の平均半径に対する割合、
つまり、OF₁÷OAを「離心率」と呼び、eで表します。
半周するのにかかる時間が最も短くなるのは
ケプラーの第2法則(面積速度一定の法則)から
月が点Eから点Gに移動する時間
つまり、上図1の色付きの部分であると言えます。
この面積が楕円の全面積に対して
どれだけの割合かを調べれば良いわけです。

細かな導出は省略しますが、
図2のように円を使って計算するとやりやすいです。
図2の色付きの部分と半円の面積の差を
近似すると2e/πとなります。

月の場合e=0.055となりますから
公転周期T=27.3日を用いると
月が地球の周りを半周するのにかかる日数の最小値は
公転周期の半分より約1日ほど短いことがわかります。

以上により、先日ブログに書いた内容は
ほぼ正しそうだと言えそうです。  

日本では、中秋の名月だけでなく
翌月の十三夜も見ないと風流ではないそうです。

十三夜は「満月より少し欠けていて綺麗だから」
という説がよく言われていますが
「月の背景にある星空がほぼ同じになる」
という説があるようです。

時計の長針と短針が出会う間隔は
1時間より少し長くなりますが
満月から満月になるまでの時間が
ちょうどそれに当たります。
これを「朔望月」と言います。
時計の中心＝太陽、短針＝地球、長針＝月というわけです
(短針・長針の長さの関係を逆にして、なおかつ
短針の先を中心に長針が回転しているような
時計を想像すると点と良いでしょう)。

これに対して
短針や長針が一周する時間が「公転周期」です。
月の公転周期は27.3日ですが
中秋の名月からほぼ27.3日経ったのが
今日ということになります。
時計に例えて言うなら、9時49分頃の
短針と長針が重なったときが「中秋の名月」、
その1時間後の10時49分頃が「十三夜」、
その数分後の10時55分頃が満月ということになります。

池の周りを2人がぐるぐる歩く問題を
数学の時間に習ったことでしょうが、
公転周期から朔望月を求めるのにはこれを使います。
月の形なんて生きるのに関係ないかもしれませんが
ちょっと深く知ろうと思ったら
数学とかも必要なんですよね。  

大雑把に言えば「中秋の名月」は
「新暦9月に見える満月」と言えますが
厳密には違うようです。

地球から見て太陽と月がまったく同じ方向に
見える瞬間を「新月」と呼び、月齢を0とします。
24時間ごとに1ずつ月齢は増え、
次の新月の時に月齢は0に戻ります。
新月の瞬間を含む日を旧暦では1日、
その翌日を2日、…としましたので、
ほぼ旧暦の日付＝月齢+1が成り立ちます。

今年9月5日午後9時(日本時間)に新月になりました。
したがって9月5日は旧暦8月1日で、
今年9月6日(旧暦8月2日)午前9時の月齢は0.5となります。
新聞には通常その日の正午での月齢が書かれるようです。
旧暦8月15日(つまり月齢が14になる瞬間を含む日)の
夜に見られる月を“中秋の名月”と呼びます。
今年は9月19日が中秋の名月になります
(正午の月齢は13.6、午後9時の月齢は14.0です)。

地球から見て太陽と月が180ﾟ反対方向に
見える瞬間を「満月」と呼びます。
新月から次の新月、あるいは満月から次の満月まで
29.53日間かかりますが、月は楕円軌道を回っており
厳密には一定の速さではないため、
新月から満月までの日数は半分の14.8日間より
1日少ないことも1日多いこともあります
(これについてはこちらで検討しています)。

つまり満月の瞬間での月齢は平均すれば14.8ですが、
13.8になることも15.8になることもあるわけです
(ケプラーの法則で速さは決まりますから
地球を半周するのにかかる時間には
上限と下限が存在する筈です)。

新月の瞬間から14.8日後のところに
頂上がある山を想像してみましょう。
新月の瞬間は「新月の日」の0時から23時59分まで
均等に起こる筈ですから、
山の頂上は「新月の日」の0時から見て
14.8～15.8日後に分布するようになります
(山が“分身の術”を使っている感じですね)。
となると、最も満月になる確率が高い日は
新月の日の0時から見て15日後になる筈です。
それで「十五夜」というわけですね。

今年は9月19日午後8時(月齢14)に満月になり、
満月の日と中秋の名月が重なりました。
次回は2021年だそうです。  

遺伝の勉強のとき、親をP、子を1、孫をF2、…と書きますね。
農業をされている方はF1はよく使うようです。
PもFもラテン語が起源の言葉です。

Pは英語と同じparentです。
entは人を意味する語尾ですが、
pareは「整える」というような意味のようです。
ニュアンス的には「生み出す」「力をもたらす」のようで
画竜点睛のエピソードの「目を入れる」に近いのかもしれません。
だからparentは「子どもを生み出す人」ということですね。
pre(前もって)が付けばprepare「準備する」になります。
準備したものがpreparat「プレパラート」(ドイツ語)です。
emperor「皇帝」も元は“隊列を整える人”という意味だそうです。
compare「比較する」のpareは別物でpairと同語源です。

Fはfiliusというラテン語だそうですが
英語にも関連語彙が無いか調べてみました。
ad libとかのad(～に向かって)が変化した“af”が前にくっついて
動詞化したものがaffiliate「加入させる」だそうです。
ネットで稼ごうというあの話の“アフィリエイト”です。
元々は「養子にする」という意味から派生したんだとか。
だから「嫡出子の父親を決定する」という法律用語もあるみたい。
「“加入させる”から“認知する”」とこじつけて
覚えている人もいるかもしれませんが
やはり語源を考える方が説得力ありますね。

うちの塾も今春から予備校部門ができますが
こういう授業をやったら面白いですよね。
もし英語力があったら立候補するんですけどね(笑)  

高校などで習う「半減期」とは
原子核で起こる壊変に関する値であり
ある時期に物質に含まれる同位体の量をf(t)とすると(t>0)
f(T+t)=f(t)/2が常に成り立ち、このTのことを「半減期」と呼びます。
これは同位体の量が指数関数的に変化することを示す言葉です。

私が「生物学的半減期」という言葉を初めて聞いたのは
たぶん3.11以降のことだと思いますが
生物における反応なのに
指数関数になるのだろうかと疑問に思いました。

調べてみると、ヨウ素の生物学的半減期は
甲状腺とそれ以外では10倍の差があるようです。
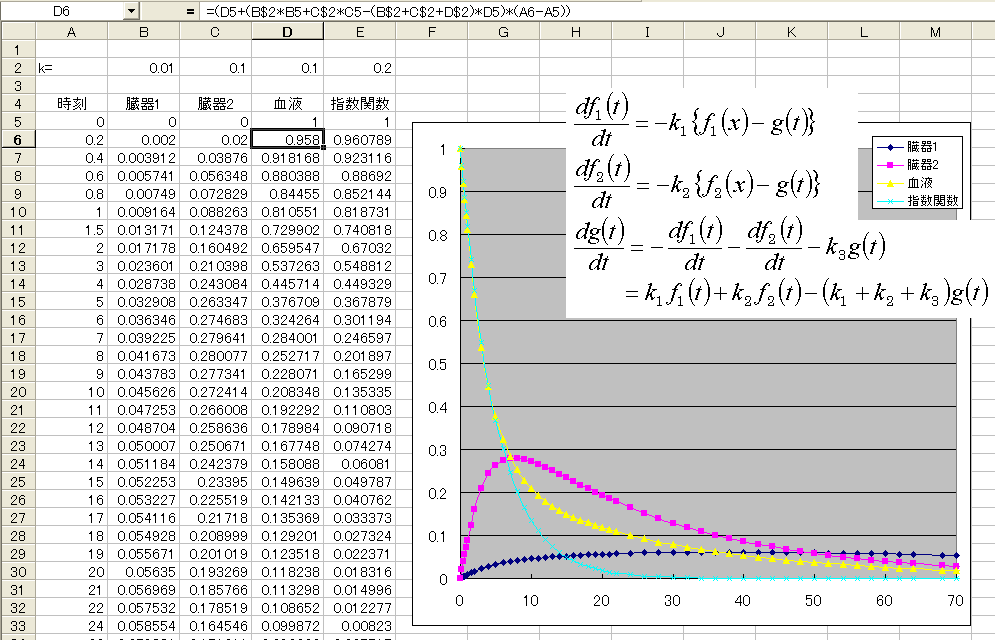
そこで、透過度k₁,k₂の半透膜袋(臓器に相当)を
水槽(血液に相当)に入れたとして挙動を計算してみました。
「コンパートメントモデル」と呼ばれるものっぽいです。
肝臓や腎臓で処理され血液内から消えてく速さがk₃。
膜から出ていくのも入ってくるのも同じ速さとしました(濃度差に比例)。

f₁(t)とf₂(t)が臓器に含まれる物質の量
g(t)が血液に含まれる物質の量です。
血液から物質が入るのが普通と考えられるので
f₁(t)=f₂(t)=0,g(t)=1としました。

式は下図に入れておきました。
本当は3番目の式に体積を考慮した変数を入れないといけないのだけれど
今は「指数関数になるか」を確かめるだけなので
臓器1と2、血液の体積は全て同じものとしています。

数値は適当に決めたものです。時刻も秒とは限りません。
ただ半減期が10倍違う臓器を設定しているモデルだということです。
また物理的半減期を考慮していないので、放射性元素の挙動ではありません。

水槽の中の物質は濃度に比例した分、徐々に減っていきます。
もし「半減期」の名前どおり指数関数になるとしたのが水色。
t=0の近傍ではy=exp{-(k₁+k₂+k₃)t}が漸近線らしい。

グラフの縦軸を対数にしたのが、次のグラフ

黄色は水色と一致していないのですから
この場合「半減期」という考え方は幻想だと言えます。

でも2番目の対数グラフで、黄色はほぼ直線に近づいていますから
「ほぼ指数関数」と言えないことはないかもしれません。
しかし「きれいに」なのか「ほぼ」なのかは大事な違いです。
下手をすると黄色の線を水色の線のように過小評価されてしまうのですから。

各臓器の半減期に差が無ければ、最終的には指数関数に近づきます。
なので物質によっては良い結果を得られるのでしょうが…。
物理的半減期と違って「どこから半分になる時間なのか」が大事なようです。
そして「どこまで、その半減期を使っても支障がないか」の注意も必要。

ていうか、こんな簡単なことに誰も気付かないとしたら問題ですよね?
皆さんはこの辺りまで「生物的半減期」の考察をしましたか?
私が何か間違っているのだったら教えて欲しいです。
そして、できれば、誰かに微分方程式を解いてほしいです。

【注】上に「ヨウ素」と書きましたが
放射性ヨウ素の物理的半減期は約8日であり
仮に生物学的半減期の考えが仮に間違いとしても
8日を越えることは無いと考えます。
問題とすべきは、
物理的半減期がもっと長い放射性元素が
特定の臓器に滞留する場合
生物学的半減期による計算によって
過小評価されてしまうのではないかということです。

【8/29追記】1か月以上経って
ようやく実測データを見つけました。

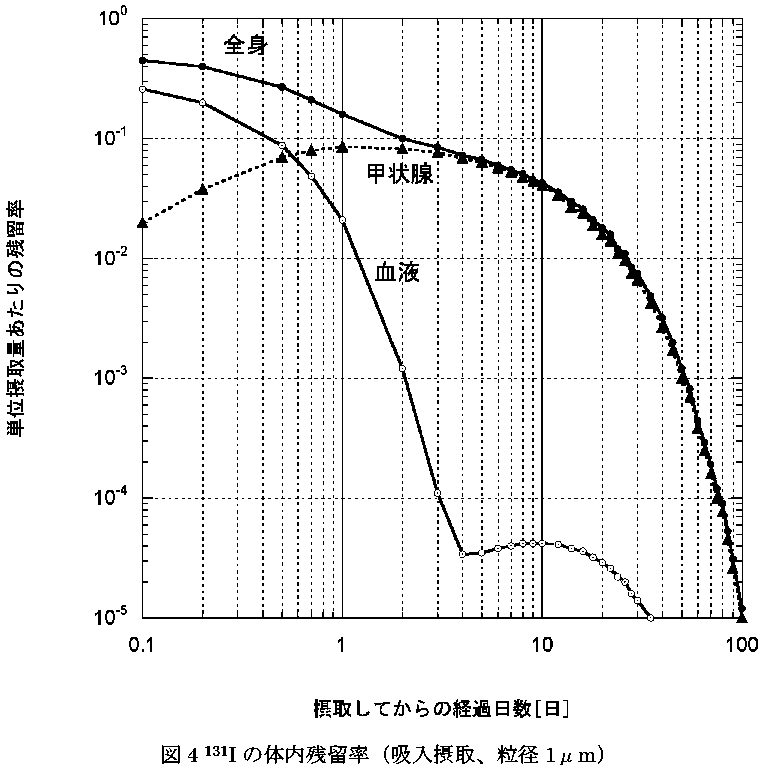
横軸も対数になっているのでちょっと違ってます。
こちらにあったものです。  

枝野さんが「ミリとマイクロは1つ違う」って言ってましたが
よくわからない人もいると思うので説明します。

知ってると思うけど「ミリメートル」というのは
「ミリ」と「メートル」からできている。
1メートル=1000ミリメートルなんてやると
学生時代を思い出すでしょ(笑)

実は「キロ」「ミリ」「マイクロ」「ナノ」は全部同じ仲間で
「メートル」とか「グラム」とか基本となる単位の前に
好きに付けちゃって構わない(「マイクロ尺」があるのかはわからんが)。
だから「マイクロアンペア」「ナノグラム」なんてのもありうる。

どんな単位に付けても「ミリ」は「1000分の1」
「マイクロ」は「100万分の1」って意味になる。
ちなみに「ミルフィーユ」とか「ミリオネア」の
“mil”は1000って意味だそうで
その後ろに“i”を付けると逆数になるって法則があるらしい。
「セント」と「センチ」もそういう関係。

例えば「私の身長は0.0015キロメートル」なんて
言う奴はいないけど、なぜかと言えば
やっぱり小数はわかりにくいからだと思う。
髪の毛は人によって違うけど0.05～0.1ミリメートルで
(紙の厚さも大体このくらいだけど同じ「かみ」なのは意味があるのかな)。
これもわかりにくいから1つずらして
50～100マイクロメートルって表してやるわけ
(ちなみにマイクロメートルは昔「ミクロン」と呼んでました)。

枝野さんの発言は「今まではメートルで表してたけど
大きくなったのでキロメートルで表してます」と
言ったのと同じような意味なわけ。  

wikipediaを見てもなんかよく分からなかったので
自分なりの解釈を書いてみたい。

わかりやすく放射能に曝されることを殴られる行為に例えるとする。
シーベルトSvとは単位だから「線量」って言わないと正しくないのだが
本来は「熱量」って呼ぶべきなのにカロリーでも通ってるから
わかりやすさ優先ってことで、シーベルトで書きます。

要するにシーベルトとは
放射性物質から受けた“パンチ”の回数ってこと。
昔は「レムrem」という単位だったが、
SI単位系の導入で変わったみたい
(ミリバールmbがヘクトパスカルhPaに変わったのと同じ理由)。

自然界からもパンチを受けているので
長く生きればそれだけパンチは受けている。
パンチを食らっても間隔が長ければ復活できるように
長い時間内にパンチを少しくらい食らっても問題無いし
少しくらいならパンチの多いところでも
短い時間内だけなら復活できちゃうってのは
感覚的に解ると思う
(もちろん相手がボクサーなら一発でアウト)。

だから現場での放射能の強さは、1時間あたりのパンチの回数で表し
人間が受けたダメージの大きさは、パンチの総回数で表す。
「時速何km」と「距離が何km」が全然違うように、
「1時間当たり」とか「/h」が付いてるか付いてないかは大きな違い。

でも「今この車100キロで走ってるよ」って言ったら時速ってわかるように
たぶん現場の人は「1時間当たり」を省略してもわかるのだろうね。
それで記者会見でも省略して言っちゃったんかな。
それかマスコミが理解してなかったか。


レントゲン(X線撮影)は、
1時間当たり約500マイクロシーベルトだそうだけど
カメラのシャッターと同じで一瞬だけX線を体に当てるから
「1時間当たり」が付いてなかったら
どれだけ大きなシーベルトになるか分かるはず
(500マイクロ÷0.0000…時間の計算になるからね)。

人間は1年当たり2.4ミリシーベルト=2400マイクロシーベルト、
つまり1時間当たり約0.3マイクロシーベルトのパンチを常に受けてるらしい。
じゃあ、1時間当たり0.5マイクロシーベルトの所は危険かと言うと
「1時間そこに居たら」って話なわけだし、仮に1時間居たとしても
その後にシーベルトの少ない所に居れば問題ないってこと。

実は医療検診を含めると日本人は
1年当たり4.4ミリシーベルト=4400マイクロシーベルト
平均する意味はあまり無いけど単位を合わせてやると
1時間当たり約0.5マイクロシーベルトになる。
これが上で述べたことの根拠。

詳しい数値(1年当たりだけど)はhttp://www.atomin.go.jp/atomin/high_sch/reference/radiation/jintai/index_06.htmlへ。
ミリとマイクロの違いはhttp://sak.naganoblog.jp/e691373.htmlをどうぞ。